| ■19■ 2つの正三角形の移動によるヘキサグラムの 6つの頂点が消えないための限界点を求めます Limit in the form of hexagram |
| <限界点の軌道が作る正三角形の一辺の長さを求める式> |
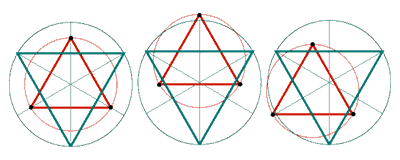
| 中心のヘキサグラム | 上部の限界 | 左側の限界 |
| ■19■ 2つの正三角形の移動によるヘキサグラムの 6つの頂点が消えないための限界点を求めます Limit in the form of hexagram |
| <限界点の軌道が作る正三角形の一辺の長さを求める式> |

| 中心のヘキサグラム | 上部の限界 | 左側の限界 |
|
|
prinityA/B/C=60/50/300<各円の直径>
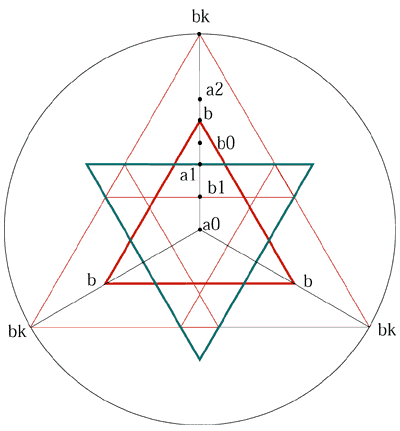
正三角形Aの一辺=30R3 正三角形Bの一辺=25R3 a0.a1=60/4=15 b0.b1=50/4=12.5 a1.b1=R3(30R3-25R3)/2=7.5 2つの正三角形の中心の移動(a0.b0)=20 円Aの半径-円Bの半径=5 ヘキサグラムの限界点(bk.a2)=15 a0.bk=45 45の円に内接する正三角形の一辺は45R3となり、これが求めるヘキサグラムの限界点の軌道をなす正三角形です。 これをプロニティーの比例式で求めると (A-B){(C/A+C/B)-(C/B-C/A)-1} 正三角形Aの一辺=30R3 正三角形Bの一辺=25R3 正三角形Cの一辺=150R3 (30-25){(150/25+150/30)-(150/25-150/30)-1}=5*(11-1-1)=45R3 |
| 正三角形bkが正三角形Bの頂点bが動く ヘキサグラムの限界点です。 |
|
2つの正三角形A.Bからなるヘキサグラムの形が消滅する限界点となる軌道は正三角形bkとなります。 個の正三角形の大きさは正三角形A.Bの比率が近づけば大きくなり、離れると小さくなります。 |
*PDF書類では図形を拡大して鮮明に見ることが出来ます
Copyright (C) 2010 Masaki Matsuura. All rights reserved.