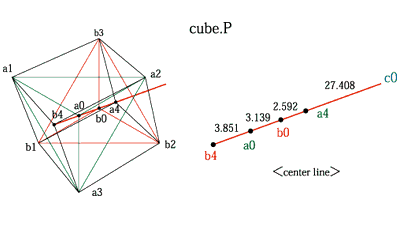
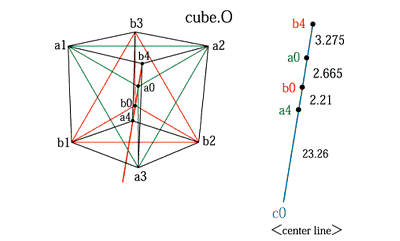
| ■10■ 3つの正三角形の中心の相対距離と立方体の頂点の距離の数値 Relative distance of center |
| 2つの正三角形の重心の距離(a0.b0)から 立方体の奥と手前の2つの頂点の距離を算出する事が出来ます。 pronityA/B/C=19.88/18/190 c0は正三角形Cの重心、距離a0.b0=xとすると (正三角形Cの重心からBの重心b0)c0.b0=xC/A x=3.662 c0.b0=3.662*190/19.88=35 (正三角形Cの重心からAの重心a0)c0.a0=xC/B x=3.662 c0.a0=3.662*190/18=38.66 |
| (正三角形Cの重心から立方体の奥の頂点a4)c0.a4=xC/{A+(A-B)} x=3.662 c0.a4=3.662*190/{19.88+(19.88-18)}=31.975 (正三角形Cの重心から立方体の手前の頂点b4) c0.b4=xC/{B-(A-B)} x=3.662 c0.b4=3.662*190/{18-(19.88-18)}=43.16 a4.b0=35-31.97=3.03 a0.b4=43.16-(3.662+3.03+31.97)=4.498 |
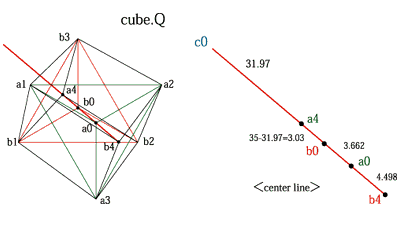
■3つの正三角形の重心と立方体の頂点の関係■ヘキサグラムを構成する2つの正三角形A.Bの重心が重なるとき、正三角形Cの重心も重なります。 A.Bの重心が距離(x)離れるとCの重心(c0)からBの重心(b0)までの距離はc0.b0=xC/Aで求めることが出来ます。 |
|
|
今度はc0からb0の距離を30とします。
|