■05■
a0.b0は2つの正四面体のそれぞれの重心で、 |
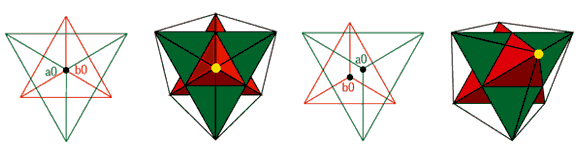
視覚空間の奥行きが生み出す立方体の形の変化(稜線の変化)と2つの正四面体からなるヘキサ立体の関係
2つの正四面体の重なっている2つの重心が離れると (a0.b0)奥と手前の頂点(a4.b4)は図のように大きく動きます(b0→b4)(a0→a4)。
この2つの点が立方体の奥と手前の頂角となり12本の稜線の長さは全て変化します。 この空間構造を立方体から逆に考える事(描く事)は出来ません。 ですから立方体が最初にあってその対角線が正四面体ではなく、 2つの正四面体が最初にあってその頂点を結ぶと立方体になると言う方が正確な表現です。
|
 |
|
|
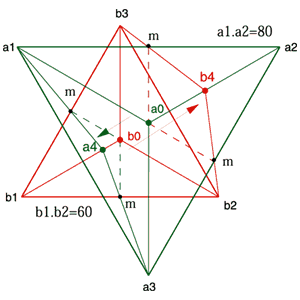
■交互に交わる3つの正三角形の頂点と中点■ 正四面体A.Bの2つの底面からなるヘキサグラムの位置関係から立方体の奥の頂点(a4)と手前の頂点(b4)の2つの頂点を求めると、その延長線は正三角形Cの3辺の中点に交わります。 このことから正四面体Bの頂点b4は正三角形Aの中点を通り、正三角形Bの頂点を通って正三角形Cの中点に交わります。
|




