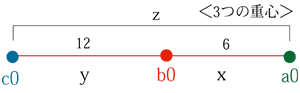
■06■ プロニティーA/B/Cと 正三角形の重心の移動と頂点の移動距離 Movement of center and moving distance of vertex |
pronityA/B/C=60/40/120
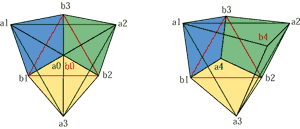
中央のグレー部分は2つの正三角形(A.B)の重心が 同じ位置の時の立方体の輪郭を示しています。 A.Bの重心(a0.b0)が離れたとき、 空間の関係はこのようになります。 |
|
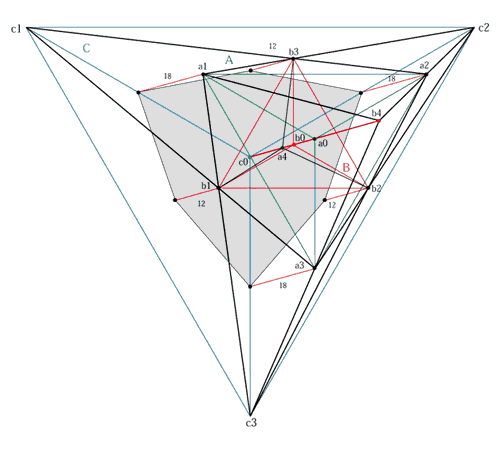
正三角形A.Bの重心(a0.b0)の距離が(x)離れたときの
立方体の手前と奥の頂点の移動数値 |
|
a0.b0が距離(x)とする時、立方体の手前の頂点b4と奥の頂点a4、そして正三角形Cの重心であるc0は(x)の距離とプロニティーの比例数によって求めることが出来ます。
|
pronityA/B/C=60/40/120 a0.b0=x ●c0.a0=xC/B● ●c0.b0=xC/A● ●c0.a4=xC/{A+(A-B)}● ●C0.B4=xC/{B-(A-B)} x=6 c0.b0=6*120/60=12 c0.a4=6*120/{60+(60-20)}=720/80=9 c0.b4=6*120/{40-(60-40)}=720/20=36 a0.b0=6 a4.b0=12-9=3 c0.a4=9 a0.b4=36-(6+3+9)=18 |
|
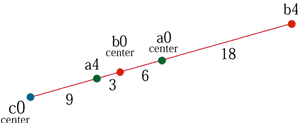
正三角形A/B/Cの3つの重心の距離関係
|
|
プロニティーの関係にある3つの正三角形の重心(a0.b0.c0)の相対距離は(a0.b0)が(c0)の位置を決定し(a0.c0)が(b0)を、(b0c0)が(a0)の位置を決定します。
|
pronityA/B/C a0.b0=x b0.c0=y c0.a0=z x=zB/C y=xC/A z=xC/B x=yA/C y=zB/A z=yA/B |