| ■NO.54■ 完全数6の約数比1.2.3.6と正三角形の辺、 面積と正四面体の体積の関係 The divisor ratio of the complete number 6 |
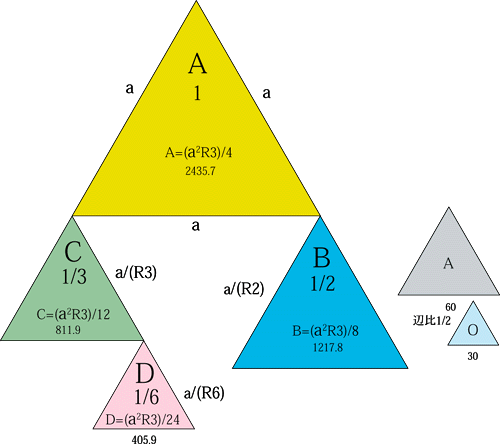
完全数6の約数比による4つの正三角形の関係
|
<1.1/2.1/3.1/6による線分と面積の関係> |
|
|
1辺(a)の正三角形の面積(A)を1とする
|
<正三角形の辺、面積の比例>
正三角形は辺比が2倍になると面積は4倍になり、 面積比が2倍になると辺はR2倍になる。 |
|
正三角形A.B.C.Dの面積比が1/2/3/6の時の4つの辺の比例
Aの1辺=a B=a/R2 C=a/R3 D=a/R6 |
|
A.B.C.Dの辺比
辺A/辺B=R2 辺A/辺C=R3 辺A/辺D=R6 辺B/辺C=R1.5 辺B/辺D=R3 辺C/辺D=R2 (辺A+B)/(辺C+D)=R3 (辺A+C)/(辺B+D)=R2 |
|
一辺Aの正三角形に対する面積比P/Aの正三角形の一辺<L>
L=A*R(P/A) 例 正三角形AのP/Aの面積を持つ正三角形Lの一辺を求める Aの一辺=75 P/A=1/2 L=75*R(1/2)=50.33 |
|
正三角形の一辺aから面積Aを求める
A=(a2乗*R3)/4 正三角形の面積Aから一辺aを求める a=2R(A/R3) |
|
一辺Aの正三角形に対する辺比P/Aの正三角形の面積<O>は
O=(A/2)2乗(P/A)2乗*R3 |
例 正三角形Aの1/2の辺比を持つ正三角形Bの面積を求める
A=60 P/A=1/2の時 B=(60/2)2乗 *(1/2)2乗*R3=389.71 |
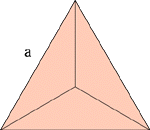
一辺aの
正四面体の体積(Av) Av=(a3乗*R2)/12 |
<正四面体の面積比1/2.1/3.1/6の体積の比例>
正四面体Aの体積に対してBは1/(2R2)倍、Cは1/(3R6)倍、Dは1/(6R12)倍となる。 <正四面体の数値> 正三角形の一辺=a 正三角形の高さ=aR3/2 正三角形の半径=a/R3 正三角形の面積=a2乗*R3/4 正四面体の高さ=aR2/R3 正四面体の体積=a3乗*R2/12 正三角形A.B.C.Dの面積比<1.1/2.1/3.1/6> 正四面体A.B.C.Dの体積比<1.1/2R2.1/3R6.1/6R12> Aの体積=75の3乗*R2/12=596621.3/12=49718.4 A/(1R1) Bの体積=53の3乗*R2/12=210543.8/12=17578.1 A/(2R2) Cの体積=43.3の3乗*R2/12=81189.8/12=6765.8 A/(3R6) Dの体積=30.6の3乗*23R2/12=28704.9/12=2392.08 A/(6R12) |
*PDF書類では図形を拡大して鮮明に見ることが出来ます
Copyright (C) 2010 Masaki Matsuura. All rights reserved.

dream & harmony