pronity/49/完全数6とプロニティ

　 pronity_rogo

■NO.49■
完全数＜6＞の約数と立方体の空間構造のプロニティー
The divisor of the complete number <6> and the cube

立方体の体積を6とすると、
2つの正四面体からなるヘキサ立体の体積は3、
1つの正四面体の体積は2、
立方体の核となる正8面体の体積は1となり、
完全数＜6＞の約数1.2.3に対応します。

これは1辺Xの正四面体の体積は
1辺X/R2の立方体の体積の1/3と考えればいいことになり、

1辺Xの正八面体の体積は
一辺2X/R2の立方体の体積の1/6となります。

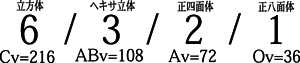
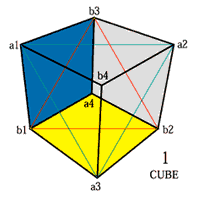
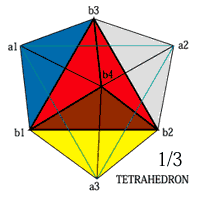
	立方体の6つの面の対角線を稜線とする正四面体はその体積が立方体の1/3となります。そして立方体と正四面体の表面積の比は、R3/3となり、それぞれ6本の稜線の比はR2/2となります。＜正四面体と立方体＞ ●体積比=1/3 ●表面積比=Ｒ3/3 ●稜線比＝Ｒ2/2
立方体の1辺=6　体積=216 表面積=216　稜線=72		正四面体の1辺=6R2　体積=72 表面積=72R3　稜線=36R2
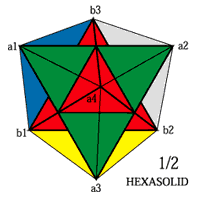
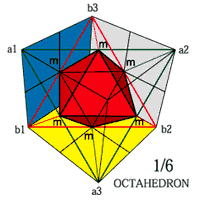
	立方体の6面の全ての対角線からなるヘキサ立体は2つの正四面体が組合わさった星形の立体です。この立体は対角線の1/2の一辺をもつ正八面体の8つの面に8つの正四面体がくっついたもので、体積が立方体の1/2、正八面体の3倍をしめます。＜ヘキサ立体と正八面体＞ ●体積比＝1/3 ●表面積比＝1/3 ●稜線比＝1/2
ヘキサ立体の1辺=6R2　体積=108 表面積=108Ｒ3　稜線=72Ｒ2		正八面体の1辺=3R2　体積=36 表面積=36Ｒ3　稜線=36Ｒ2

立方体の体積(A)と正四面体の体積(B)の積を差で割ると
ヘキサ立体の体積(C)となります。
pronityA/B/C=A*B/(A-B)=C------216*72/(216-72)=108

■立方体と正四面体の関係■

立方体の体積(Cv)はその対角線を1辺とする正四面体(Av)(Bv)の3倍となります。

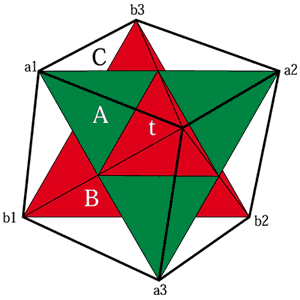
そして2つの正四面体からなるヘキサ立体の体積(ABv)の2倍、対角線の1/2を稜線とする正八面体の体積の6倍、対角線の1/2の正四面体(tv)の体積の24倍となります。

Cv=2ABv（ヘキサ立体の2倍）
Cv=3Av（正四面体の3倍）
Cv=6mv（正八面体の6倍）
Cv=24tv（1/2の正四面体の24倍）

この様に立方体と正四面体はとても簡単で美しい比例関係の中で同じ空間を共有し、分割しています。この事を理解していれば正四面体や正八面体の体積をとても簡単に求めることが出来ます。