| ■47■ 3つの正三角形の60度の自転による 鏡像のヘキサグラムと空間 Hexagram of mirror image and space |
pronity40/30/120=A/B/C
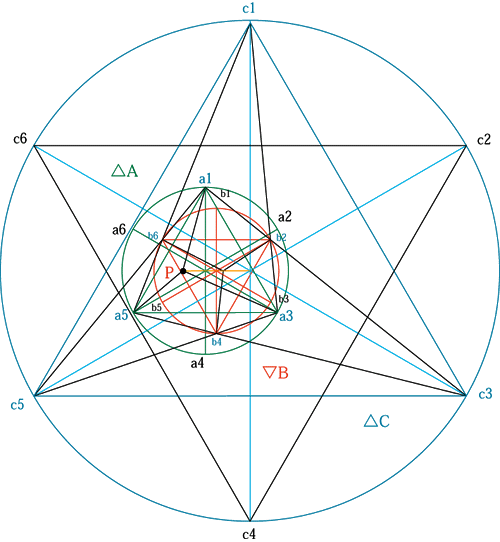
プロニティーの関係にある3つの円に内接するヘキサグラムの6頂点は、60度に交差した3本の円の直径の端点であり、3つの円に内接する3つのヘキサグラムのそれぞれの頂点を結ぶ放射線の関係は、3つの円周上の6分割された点と点の関係に同じである。 円Aの3点(a1.a3.a5)と円Bの3点(b2.b4.b6)を連続して結んで出来る6角形の各辺の延長線は、2本づつ円Cの3点(c2.c4.c6)に交わる。この関係は三角形A.B.Cで見ると逆.正.逆の正三角形の頂点を結ぶ関係となる。 又、直径の端点として円Aから順に見ると円Aの点a1、円Bの点b2を結ぶ線の延長が円Cの点c3に交わり、a3とb2を結ぶ線はc1に、a5とb6を結ぶ線はc1へと言うように、A.B.Cの3つの円周上の60度づつ回転した3つの点を結ぶ線分となる。
|
|
|
<1と2は180度回転した鏡像> |
<円A.B.Cの各6つの相対点> |
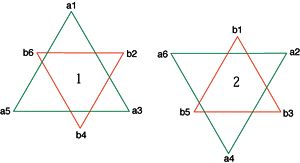 |
a3/b2/c1 a4/b0/c1 a5/b6/c1 a4/b3/c2 a5/b0/c2 a6/b1/c2 a1/b2/c3 a5/b4/c3 a6/b0/c3 a1/b0/c4 a2/b3/c4 a6/b5/c4 a1/b6/c5 a2/b0/c5 a3/b4/c5 a2/b1/c6 a3/b0/c6 a4/b5/c6 |
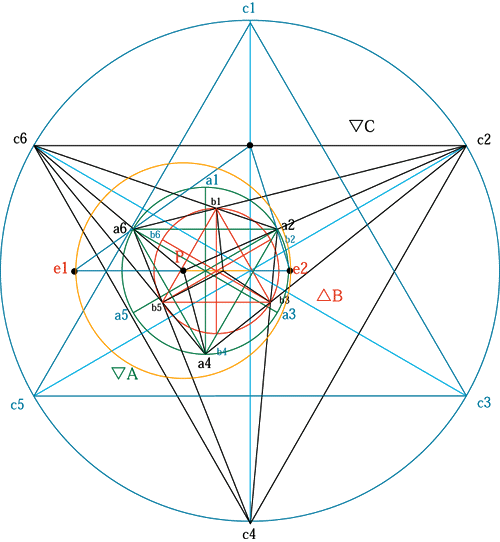
pronity20R3/15R3/60R3=A/B/C 正三角形Cの頂点c6.c2と正三角形Aの頂点a6.a2の頂点を結ぶ線の交点Pは、線分e1.e2の中点であり、3本の線分はプロニティーの関係にあり、線分e1.e2の長さは、C.Aの積を差で割って求められる。 CA/(C-A)=30R3 e1.e2=30R3 |
|
*PDF書類では図形を拡大して鮮明に見ることが出来ます
Copyright (C) 2010 Masaki Matsuura. All rights reserved.

dream & harmony

