| ■16
■ ヘキサグラムの移動による立方体の稜線の変化と数値 Change of ridge of cube and numerical value |
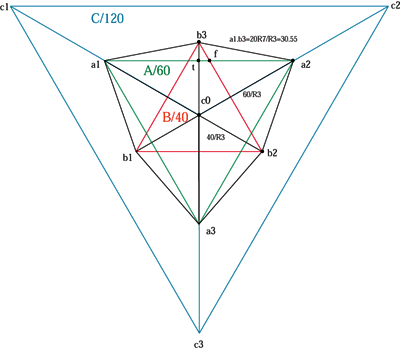
2つの正三角形が中心の時の立方体の稜線の値
立方体が中心に位置する時、手前となる稜線3本は60/R3、奥の3本の稜線は40/R3であるが、輪郭となる稜線の1辺(a1.b3)は、a1.tとb3.tの値からピタゴラスの定理で求めると、a1.b3=R{(a1.t)2+(b3.t)2}=30.55となるが、pronityA/B/Cを使えば、3つの正三角形の数値だけで簡単に求める事が出来る。 a1.b3=
b3.f={B-(A-B)}/3
線分a1.b3をピタゴラスの定理で求める |
 |
|
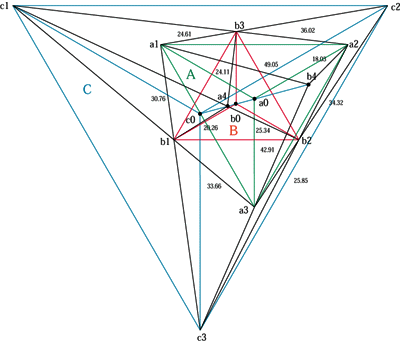
正三角形A.Bが相対的に、15度の角度で6mm移動した時の稜線の変化
|
|
pronity60/40/120.center
手前の稜線(c0.a2)=60/R3 |
 |
 |
pronity60/40/120.15de6mm
60/40/120=A/B/Cとしa0.b0=xとした時 |
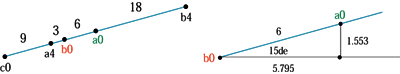
| <3つの正三角形の重心と頂点> | <点a0の移動数値> |



