ren |
同じ形が同一空間に連なるだけでも無限に異なるパターンが生まれてきます。これが奥行きをもつ3次元空間で重なると平面とは又異なった性質のパターンとなりパターンの相対する点と点を結ぶ直線は奥行きを持つ放射線となります。
|
|
<これは2次元のパターンが出来る1例です>
|
|
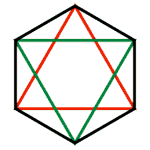
1つの正六角形(P)
1つの正六角形の回りに6つの正六角形が配置されて 1つのパターンとなります。 頂点が一致したパターン(PA)と 辺が一致したパターン(PB)の2通りが出来ます。 |
|
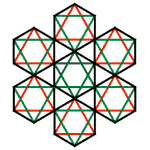
7つの正六角形が集合したパターン(PA)
このパターンを更に集合させるとそれぞれ4種類のパターンが生まれます。PAa.PAb.PAc.PAd
|
|
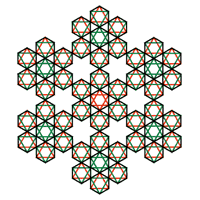
49個の正六角形が集合したパターン(PAd)
343個の正六角形の集合からはそれぞれ10種類の新しいパターンが生まれます。これは(PAd.3)です。
|

以上の操作の繰り返しから個性を持った美しいパターンが無数に生まれます |




