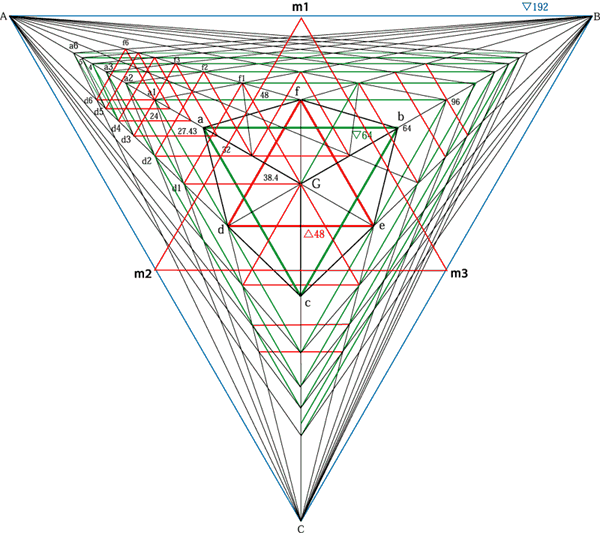
中央の正三角形abcとdefの頂点を結び延長すると正三角形ABCを得ることが出来ます。この正三角形ABCの頂点は中央の立方体(abcdefG)の3方向への消点となり、

2つの正三角形（ヘキサグラム）を基準にして、空間をあらゆる方向に分割する事が出来ます。正三角形

---

ABCに内在するヘキサグラムabcdefのdefが最大でm1.m2.m3の位置に来たとき、相対する正三角形abcはABCとなり立方体の6つの頂点のうち3つが消滅します。ですから正三角形ABCは極限の立方体の形と言うことが出来ます。

正三角形ABCの大きさがヘキサグラムabcdefに対して極めて大きい場合を考えると、この空間はその小さなヘキサグラム(abcdef)に対しては全方向に対して無限と感じるほどの空間を与えることになります。

例えば正三角形ABCの一辺が10000ｍの空間に、一辺が1ｍｍの立方体abcdefGが中央に位置するとします。そして上図で言えば正三角形ABCは視覚のはるか外で認識出来ないものとすると、この正三角形ABCの空間から脱出するのに最短の方向はもう解らなくなります。

何故なら3方向に収束する放射線の角度は平行線に近いほど緩く認識できないからです。本当は3つの中点(m1.m2.m3)に向かうのが最短の距離ですが、放射線の収束を感じられない限りそれは不可能です。