■NO.03■ 直角三角形によるヘキサグラムとプロニティ Hexagram with right triangle |
|
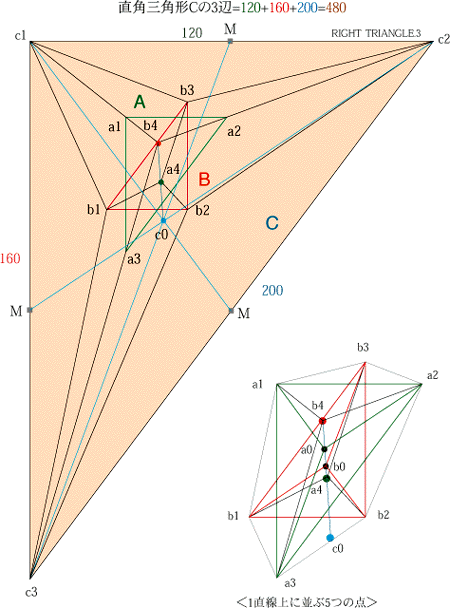
2つの相似直角三角形(A.B)をキサグラム型に配置した時の頂点と頂点を結ぶ延長線上に出来る3つの焦点を結ぶ三角形(c1.c2.c3)はともに相似形となります。
|
|
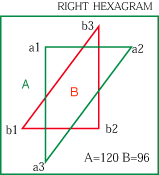
大きさの違う直角三角形(A.B)をヘキサグラム型に配置するとき、直角三角形の6つの頂点を結んで出来る6角形の3組の対辺を延長して出来る3つの交点を結ぶ形は直角三角形(C)となり、その形は相似形となる。 そして直角三角形(C)の各辺の数値は、(A.B)の各辺の数値から求めることが出来る。 |
|
3つの直角三角形の対辺のプロニティー
|
2つの直角三角形
|
|
b1.b2/a1.a2/c1.c2=pronity24/30/120
b2.b3/a1.a3/c1c3=pronity32/40/160 b1.b3/a2.a3/c2.c3=pronity40/50/200
|
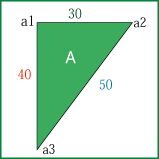
<直角三角形Aの3辺>
30+40+50=120
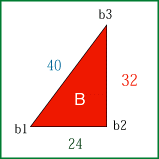
<直角三角形Bの3辺>
24+32+40=96
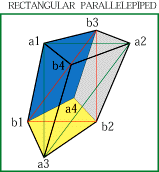
大きさの違う相似である2つの直角三角形(A.B)によるヘキサグラムは縦、横、高さに直角三角形の3辺の比を持つ直方体の収束図となり A.Bが同じ大きさの時、直方体の12辺は4本づつ3組の平行線となる
120*96/(12096)=480=CA*B/(A-B)=C辺の総和とプロニティー2つの直角三角形A.Bの辺の総和の積を,差で割ると直角三角形Cの辺の総和となる
|
*PDF書類では図形を拡大して鮮明に見ることが出来ます
Copyright (C) 2010 Masaki Matsuura. All rights reserved.

dream & harmony
![]()