pronity/02/ヘキサグラムと消点/focus

propotion of trinity

■02■
ヘキサグラムと消点の正三角形が作るプロニティの法則性
Vanishing point of hexagram

2つの正三角形A.Bをヘキサグラムの形に置いた時、
その頂点と頂点を結ぶ線を延長すると
3点で交わります(C1.C2.C3)。

この3点を結ぶと正三角形Cとなり
この3つの正三角形A.B.Cの3体の正三角形を{プロニティ}と呼びます。
pronityA/B/C=80/60/240
a1.a2=80 b1.b2=60 c1.c2=240

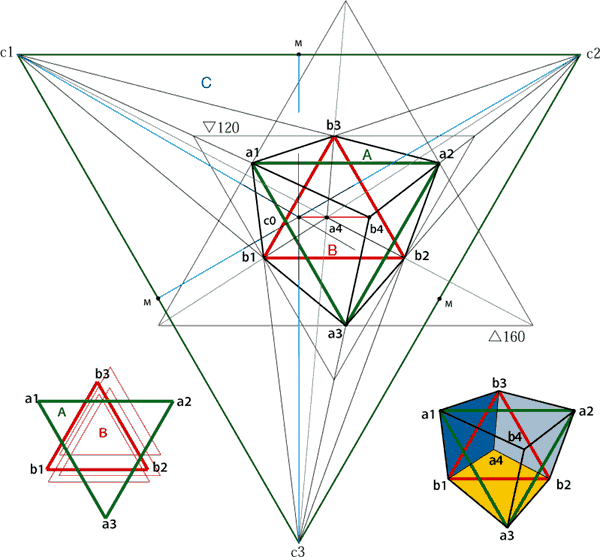
ヘキサ立方体

3つの正三角形A/B/Cがつくる
空間の三位一体の法則性

■2つの正三角形A.Bからなるヘキサグラムの頂点を結ぶ6本の線分の延長線は2本ずつ3方向に収束し、正三角形Cをつくります。

■正三角形Aと正三角形Bの大きさの比率が正三角形Cの比を決定します。

■正三角形AとBの相対的な位置関係が正三角形Cの位置を決定します。

3体の正三角形の大きさは
プロニティーの数式で求めることが出来ます

C=AB/(A-B)
B=AC/(A+C
A=BC/(C-B)
A=80 B=60 C=80*60/(80-60)=240

*PDF書類では図形を拡大して鮮明に見ることが出来ます

freedom
dream & harmony