逆正三角形A(a1.a2.a3)=70　正三角形B(b1.b2.b3)=60
2つの正逆の正三角形A.Bの比は同じ大きさ(同じ空間)の正三角形がある奥行きをもって相対的に離れた時の遠近比です。

この2体の遠近比がこれらの焦点となる正三角形Cの大きさ(第3の遠近比)を決定します。　

C=AB/(A-B)

そしてA.Bの相対的な配置が正三角形Cの位置を決定します。

a0.b0=x　c0.a0=xC/A

この正三角形Cの3つの頂点は2つの正三角形A.Bの相対する座標を結ぶ直線の焦点となり、視覚次元での3消点に対応します。

言い換えるとこのCの3頂点からAあるいはBの各点に対して引かれた直線は必ずもう一つの(AあるいはB)正三角形の相対点を通ると言うことでもあります。

点a1はA の正三角形パターン(AP)上にある点です。この点から3方向に角度と距離を合わせた3点(a04.a01.a02)を結びます。

次にこの点a1から引いた3本の線をBの正三角形パターン(BP)上に移します。AP上の点a04はBP上では点2b1に移行します。

同様に点a01はb3に、a02はb1に移行されます。点a1とこのBP上の3つの点(2b1.b3.b1)を結んだ線が

A次元からB元に向かう奥行きをもつ3本の線です。

AとBのマトリックスの重なりのズレと大きさが
この3方向への直線の収縮率を決定します。

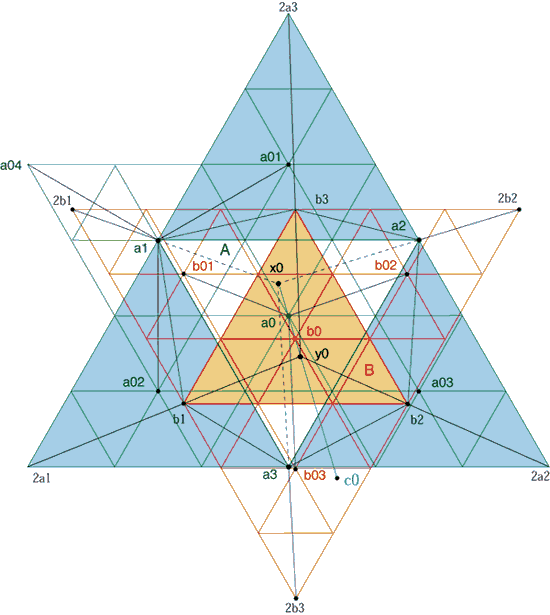
中央の2つの正三角形AとBはBがAからa0.b0の距離と角度を持って空間的に後退した状態をあらわしています。（正三角形の大きさの差が奥行きに対する比例です）A=70 B=60

点x0は前述のA次元の点a1からの線が奥に向かうのではなく手前に来たときの点です。(手前のx次元）