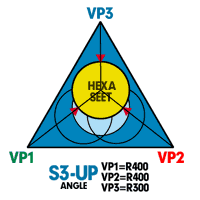
HEXAGRAPHICS/zuhou3/立体+平面=ヘキサグラフィックス

■見上げのＳのアングルで描くバラガンの3つの塔■
どんな造型でも、違った角度から見ると思わぬ発見があります。
特に建築は、底からの見上げの状態で見ることは基本的にはないですから、
フォルムや構造の思わぬ再発見があります。

カリキュラムで取り上げた他の5つの造型も、このテーマと同じ方法で描きます。

ヘキサグラムマジックのメインページに戻る

今や自然エネルギーを有効に使えるだけの科学力があります。
原発を完全に無くし、
化石燃料をなるだけ減らして行くことが未来に対する人類共通の責任です。


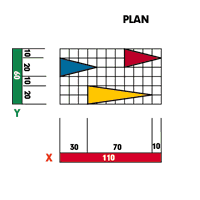
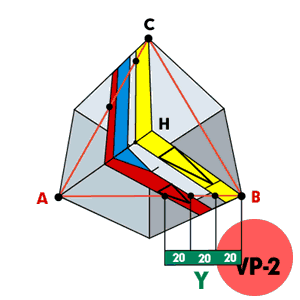
■1■平面のX方向の数値■正三角形ABCのAB線上にAから平面のX方向の実数を取り、そのポイントを通る放射線をVP1から求める。この時放射線と線分HBの交点を通る放射線をVP3から立ち上げておきます。	■2■平面のY方向の数値■正三角形ABCのAB線上にBから平面のY方向の実数を取り、そのポイントを通る放射線をVP2から求める。これで■1■との交点を結べばオブジェの平面が完成します。

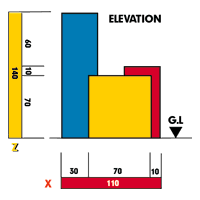
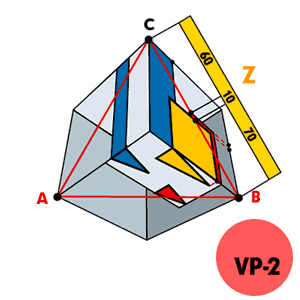
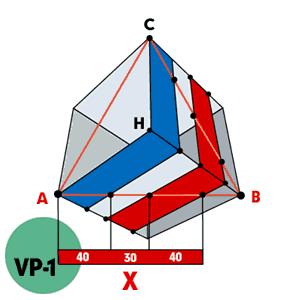
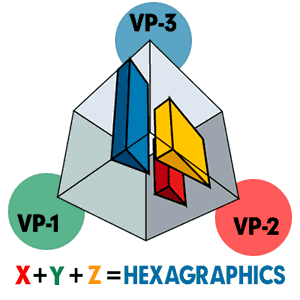
■3■高さZの数値■正三角形ABCのBC線上にBから高さZの実数を取り、VP2からの放射線を求めます。この時、平面■1■2■で立ち上げて置いた線分との交点からオブジェの立面を完成します。	■4■ヘキサグラフィックスの完成■完成した平面の各ポイントと立面の各ポイントの対応する部分を結べばヘキサグラフィックス▲S3/UP/ANGLE▲の完成です。